Adaboost最基本的性质是它能再学习过程中不断减少训练误差。
定理1 Adaboost的训练误差界
定理:Adaboost算法最终分类器的训练误差界为:
这里$G(x)=sign(f(x))\;\;;f(x)=\sum_{m=1}^{M} \alpha_{m} G_{m}(x)\;\;;Z_{m}=\sum_{i=1}^{N} w_{m i} \exp \left(-\alpha_{m} y_{i} G_{m}\left(x_{i}\right)\right)$
证明:
对于左边,当$G\left(x_{i}\right) \neq y_{i}$时,$y_{i} f\left(x_{i}\right)<0$,故而$\exp \left(-y_{i} f\left(x_{i}\right)\right) \geqslant 1$,
这边的I实际上是下面这个函数: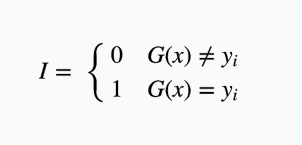
所以前半部分很显然。
关于后半部分:
首先我们知道:
自然有:
那么我们把$f(x_i)$带进去:
由于$\frac1N$是$w_{1i}$,所以根据递推式能够一步步往下推:
\begin{aligned} &=\frac{1}{N} \sum_{i} \exp \left(-\sum_{m=1}^{M} \alpha_{m} y_{i} G_{m}\left(x_{i}\right)\right) \\ &=\sum_{i} w_{1 i} \prod_{m=1}^{M} \exp \left(-\alpha_{m} y_{i} G_{m}\left(x_{i}\right)\right) \\ &=Z_{1} \sum_{i} w_{2 i} \prod_{m=2}^{M} \exp \left(-\alpha_{m} y_{i} G_{m}\left(x_{i}\right)\right) \\ &=Z_{1} Z_{2} \sum_{i} w_{3 i} \prod_{m=3}^{M} \exp \left(-\alpha_{m} y_{i} G_{m}\left(x_{i}\right)\right) \\&=\cdots \\ &=Z_{1} Z_{2} \cdots Z_{M-1} \sum_{i} w_{M G} \exp \left(-\alpha_{M} y_{i} G_{M}\left(x_{i}\right)\right) \\ &=\prod_{m=1}^{M} Z_{m} \end{aligned}
这个定理告诉了我们一件事:在每一轮选取适当的$G_m$可使得$Z_m$取到最小,从而使得训练误差下降最快。
定理2 二分类问题Adaboost的训练误差界
这里$\gamma_{m}=\frac{1}{2}-e_{m}$。
证明:
首先将$Z_m$改写一下。
\begin{aligned} Z_{m} &=\sum_{i=1}^{N} w_{m i} \exp \left(-\alpha_{m} y_{i} G_{m}\left(x_{i}\right)\right) \\ &=\sum_{y_{i}=G_{m}\left(x_{i}\right)} w_{m i} \mathrm{e}^{-\alpha_{m}}+\sum_{y_{i} \neq G_{m}\left(x_{i}\right)} w_{m i} \mathrm{e}^{\alpha_{m}} \\ &=\left(1-e_{m}\right) \mathrm{e}^{-\alpha_{m}}+e_{m} \mathrm{e}^{\alpha_{m}} \\ &=2 \sqrt{e_{m}\left(\mathrm{1}-e_{m}\right)}=\sqrt{1-4 \gamma_{m}^{2}} \end{aligned}
至于不等式
则可先由$e^x$和$\sqrt{1-x}$在点$x=0$的泰勒展开式推出不等式$\sqrt{\left(1-4 \gamma_{m}^{2}\right)} \leqslant \exp \left(-2 \gamma_{m}^{2}\right)$
进而可以得到一个推论:
如果存在$\gamma>0$,对所有的m有$\gamma_{m} \geqslant \gamma$,则:
这个推论可以说明在此条件下,Adaboost的训练误差是以指数速率下降的,这当然是一个非常好的性质。