递归和回溯法总结

在实现递归与回溯算法的时候总结了以下的几大类。

排列

排列这类问题一般需要考虑顺序，也就是说如果是寻找数字类的题目，那么对于排列来说，112和211是两个序列。而回溯法天然就有一层顺序在，所以使用回溯法来解决排列问题是很自然的。

当序列没有重复数字的时候，可以直接使用递归回溯。
当序列有重复数字的时候，需要注意对于递归树来说，同一层不能开两个数字一样的分支，否则会重复，解决这个问题一般是先对数列进行排序，使得相同数字在一块，然后用一个变量记一下上一步的数字，如果和当前数字相同那么就continue出去，否则继续向下走。

即可解决排列问题。

相对于排列类问题，组合类问题不考虑顺序，也就是说112和211对于组合问题来说是一样的。
所以组合问题主要解决的就是一个去重的问题。这个问题一般使用一个start参数来控制每次递归的开始的位置。
假设输入是1、2、3、4，递归的过程是：

start=0，所以从1开始
1
1 2
1 2 3
1 2 4
1 3
1 3 4
1 4
start=1 从2开始
2
2 3
2 3 4
2 4
start=2 从3开始
3
3 4
start=3 从4开始
4

这样控制的作用就是，第一层递归树上出现了1、2、3、4，那么在第一层选了2的第二层递归树上就不能出现1了，否则就不符合组合的定义了。

上面的情况是针对组合中没有重复的数字，如果组合中存在重复的数字，比如112这个序列，按照上面的说法它的递归过程如下。

start=0
1
11
12
112
start=1
1
12
start=2
2

很明显存在重复，重复的问题和上面排列的问题是一样的，就是同一层不允许分相同的支出来，所以实际的过程应该是这样的：

start=0
1
11
12
112
start=1 删除
start=2
2

做到这个步骤也很容易，和上面排列的做法一致，先对数列进行排序，使得相同数字在一块，然后用一个变量记一下上一步的数字，如果和当前数字相同那么就continue出去，否则继续向下走。

所以组合问题总结起来就是：start+排序

二维平面问题是回溯法的一种扩展，通常和深度优先搜索关系更大。
针对一个二维平面的问题，首先有几点是很明确的：

需要设定一个移动的顺序，来确定当前位置如何移动。比如：

1 2	# 小技巧分别表示左下右上 self.directs = [(-1, 0), (0, 1), (1, 0), (0, -1)]

1 2	def in_boundary(self, x, y): return x == 0 or x == self.m - 1 or y == 0 or y == self.n - 1

然后对于二维平面问题的解法并不统一，有的需要每次回溯，有的类似染色问题，只要访问过即可不需要每次都回溯。
这类问题包含：
130. 被围绕的区域
 200. 岛屿数量
 79. 单词搜索
417题思路非常的巧妙，它是利用了一种反向的思维，多次深度搜索来解决问题的。
417. 太平洋大西洋水流问题

比如N皇后问题也可以使用回溯法来解决：
51.N皇后

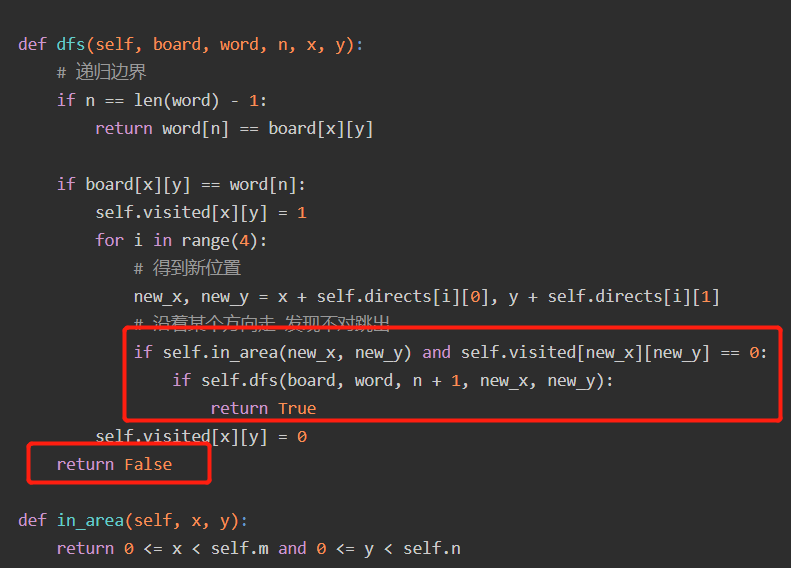
大部分回溯算法题目返回的都是空，也有一些是返回一个布尔值的，比如第79题：
79. 单词搜索
这道题返回的就是一个布尔值，递归树我们可以画成这样：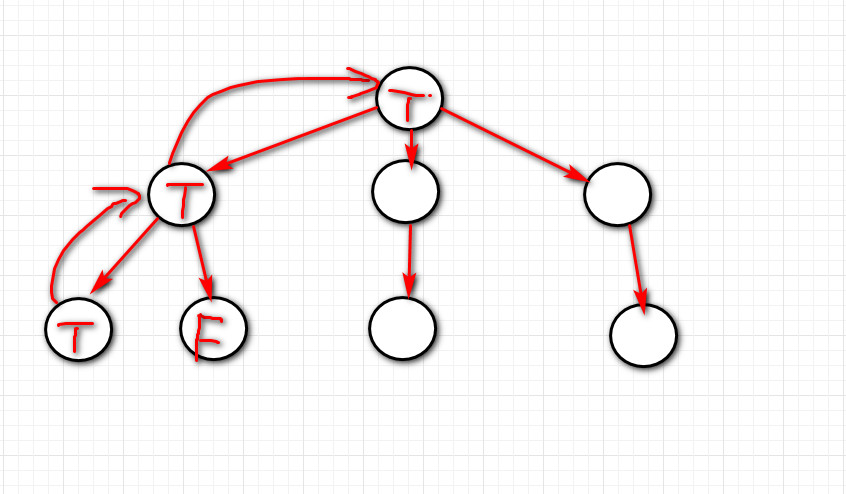
Alt text

类似于这类题目，如果有返回值它只能判断是否存在，而不能判断有几个的问题。主要思路是，第一层节点是否存在依赖于第二层是否存在，同样的一层层传递，如果发现存在了整个节点返回True，如果不存在只能等达到递归边界，返回False。
而实现这样的功能主要在：
Alt text