预备知识
内积
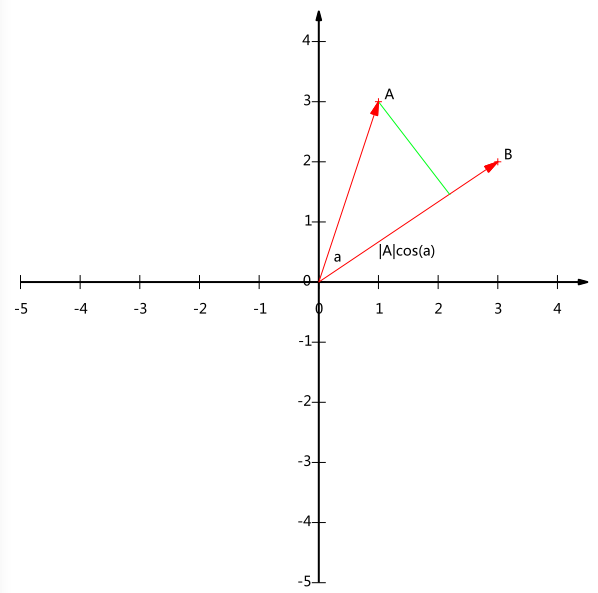
两个向量A,B内积,我们知道形式是这样的:
但是这样我们并看不出来它的物理含义,我们换成这个式子:
如果此时B的模为1,那么也就是:
此时A和B的内积等于将A向B方向上进行投影的矢量长度。
基
基在无所不在,比如我们常说的二维空间向量(3,2),其实隐式引入了一个定义:以x轴和y轴上正方向长度为1的向量为标准。那么一个向量(3,2)实际是说在x轴投影为3而y轴的投影为2。注意投影是一个矢量,所以可以为负。
所以,对于一个向量(3,2)来说,如果我们想求它在(1,0) (0,1)这组基下的坐标的话,分别内积即可。当然,内积完了还是(3,2)。
所以我们大致可以得到一个结论,我们希望一组基向量的模长是1,这样方便我们求坐标,因为向量内积,当一个模长为1的时候,内积可以直接表示矢量投影。然后还需要这组基是线性无关的,当然,一般是用正交基,因为正交基性质比较好。
那么此时,我们做一个小练习,对于(3,2)这个点,在$\left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)$和$\left(-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)$这组基下的坐标是多少?
(3,2)分别与之内积,最后得到$\left(\frac{5}{\sqrt{2}},-\frac{1}{\sqrt{2}}\right)$这个新坐标。
基变换的矩阵表示
我们熟悉的线性代数上的求基下坐标一般是:
其中$p_i$是一个行向量,表示第i个基,$a_j$是一个列向量,表示第j个原始数据记录。
实际上也就是做了一个向量矩阵化的操作。
我们用刚刚上面的例子看一下:其中数据点是(1,1),(2,2),(3,3),基是$\left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)$和$\left(-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)$
方差
由于我们在PCA部分会中心化,所以均值为0,所以有:
协方差
也是由于均值为0了,所以我们有:
此处我们当样本数较大时,不必在意样本数m和m-1的区别,所以我们为了方便计算,分母取m。
协方差矩阵
我们举个简单的例子:一个只有两个特征的数据集,总共有n个样本,那么:
X是样本矩阵。
那么X的协方差矩阵的形式是这样的(记住,协方差是关于特征的,而不是样本的):
那么我们进行计算,得到:
现在我们已经知道了X的协方差矩阵。我们再看看$x_ix_i^T$等于什么
那么
OK,所有数学原理介绍完毕,我们开始推导。
推导步骤
假设有一组样本点,$(\boldsymbol{v}_{1}, \boldsymbol{v}_{2}, \ldots, \boldsymbol{v}_{n})$,那么我们首先对这组样本点中心化,我们也知道,我们的目的是让均值为0,方便我们计算。中心化后,样本点为$(\boldsymbol{x}_{1}, \boldsymbol{x}_{2}, \ldots, \boldsymbol{x}_{n})=(\boldsymbol{v}_{1}-\boldsymbol{\mu}, \boldsymbol{v}_{2}-\boldsymbol{\mu}, \ldots, \boldsymbol{v}_{n}-\boldsymbol{\mu})$
假设我们现在从一个n维降维到d维,其中n>d。这组d维的基是$w=(w_1,w_2…w_d)^T$,那么根据我们之前说的,我们样本点$x_i$在基w下的坐标是:$\left(\boldsymbol{x}_{i}, \boldsymbol{\omega}\right)=\boldsymbol{x}_{i}^{\mathrm{T}} \boldsymbol{\omega}$
此时我们的方差是:
我们定睛一看,这个不就是我们样本的协方差嘛
我们令这个矩阵为Σ。
最终我们得到了我们的最优化问题,找到一个最优的基w使得,使得我们的方差最大。
那么我们的原问题可以写成:
其中这里由于w是基,所以有$w^Tw=1$
然后我们构造拉格朗日函数,
然后对$\omega$求偏导,得到:
此时我们的方差:
马上就会发现,原来,x投影后的方差就是协方差矩阵的特征值。我们要找到最大的方差也就是协方差矩阵最大的特征值,最佳投影方向就是最大特征值所对应的特征向量。次佳投影方向位于最佳投影方向的正交空间中是第二大特征值对应的特征向量,以此类推。
PCA求解步骤
至此我们得到了PCA的求解步骤:
(1)对样本数据进行中心化处理。
(2)求样本协方差矩阵。
(3)对协方差矩阵进行特征值分解,将特征值从大到小排列。
(4)取前d大的特征值对应的特征向量作为降维后的样本点。