0/1背包问题

发表于 | 分类于 | 阅读次数：

原理

问题是：有个小偷偷东西，他的包容量是C，物品的重量weight和价值对应value，请问小偷应该怎么偷才能获得价值最大的东西。

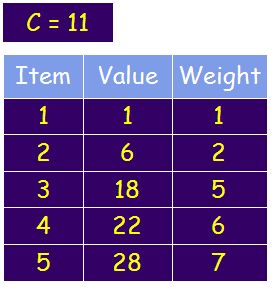
Alt text

这篇文章中关于原理的部分讲解的非常好，0-1背包问题的动态规划算法。
大致总结下来就是：
首先我们定义一个子问题$P(i, W)$，这个子问题的意思是加入第i个物品，在容量为W的情况下的解。我们将其最优解定义为$m(i,W)$.
那么我们加入一个新的物品，在容量为w的情况下，它无非有两种可能性：

  1. 把当前物品加入进行，此时$m(i, W)=m(i-1,w) + v_i$
  2. 不把当前物品加入进来，此时$m(i, W)=m(i-1,w) $

那么对于上面这个例子，我们构建一个这样的二维表格m(i,W)如下所示：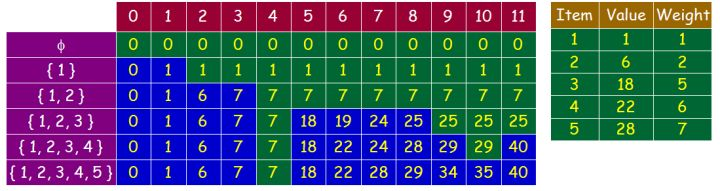
Alt text

这个表格横轴是C，从0-11，纵轴是物品，一共五件物品。

在这个问题里面我们也能恒明显的看出来：
$m(i, W) \ge m(i, W-1)$
$m(i, W) \ge m(i-1, W)$

所以一旦我们求出这个二维矩阵， 我们即可以求解出最优解。同时递推式我们也可以求解出来：

同时这个二维表还可以节省一点存储，当然上面文章中说的很对，根本的区别在于思想，而不是具体存储方式，所以使用二维表还是一维标进行存储都没有什么区别。

到这里为止，其实我们已经实现了0/1背包问题，它的时间复杂度和空间复杂度都是：

从时间上来说优化的幅度已经不是很大了，而从空间上来说仍有很多可以优化的地方。
我们看到这里其实第$i$个问题只依赖于第$i-1$个，所以我们保留两行即可，不用留那么多行。
这是一种优化空间的思路，通过余2来判断当前问题应该存在哪一行，此时空间复杂度为：

最后的一种优化空间的思路是，使用一维数组来搞定。因为我们的某一列比如上图中(5, 9)的位置，依赖于（4，2）（4，9）两个位置，所以这里有一种规律就是所有的数字都依赖于前面的，比如5，9依赖于第四行的9前面的数字，所以我们只要倒着计算即可用一维数组搞定。同时还可以减少一个常量级别的时间复杂度，因为到最后一行我们计算完了最后一个节点就可以不用接着往下计算了。最终优化后的0/1背包问题的时间复杂度是：$O(n * C)$，空间复杂度是：$O(C)$

leetcode416题经典0/1背包题

题目描述

给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

注意:
每个数组中的元素不会超过 100
数组的大小不会超过 200

1
2
3
4
5
6
7
8
9
示例 1:
输入: [1, 5, 11, 5]
输出: true
解释: 数组可以分割成 [1, 5, 5] 和 [11]. 

示例 2:
输入: [1, 2, 3, 5]
输出: false
解释: 数组不能分割成两个元素和相等的子集.

分析

首先我们将题目重新翻译一下：
给定一个只包含正整数的非空数组。是否可以从这个数组中挑选出一些正整数，每个数只能用一次，使得这些数的和等于整个数组元素的和的一半。

0-1 背包问题也是最基础的背包问题，它的特点是：待挑选的物品有且仅有一个，可以选择也可以不选择。

下面我们定义状态，不妨就用问题的问法定义状态试试看。
dp[i][j] ：表示从数组的 [0, i] 这个子区间内挑选一些正整数，每个数只能用一次，使得这些数的和等于 j。

那么当进行到第i次时，会有两种情况，一种是将第i个样本放进去，一种是不放进去。

  • 放进去num[i]，则能不能找到结果就取决于在[0，i-1]里面能不能找到一个数等于j-nums[i]
  • 不放进去num[i]，那么结果就取决于[0, i-1]里面能不能找到一个数等于j

所以最后的递推式可以这么写：

1
dp[i][j]=dp[i-1][j] or dp[i-1][j-num[i]]

同时由于下标的限制，我们也能看出来j <= num[i]

此时我们可以愉快的写代码了！

最原始的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public boolean canPartition(int[] nums) {
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        if (nums.length == 0) return false;
        if (sum % 2 == 1) return false;
        boolean[][] dp = new boolean[nums.length][sum /  2 + 1];
        dp[0][0] = true;
        // 先写第一列
        for (int i = 0; i < nums.length; i++) {
            dp[i][0] = true;
        }

        for (int i = 1; i < nums.length; i++) {
            for (int j = 0; j <= sum / 2; j++) {
                int num = nums[i];
                if (num > j) continue;
                dp[i][j] = dp[i - 1][j] || dp[i - 1][j - num];
            }
        }

        return dp[nums.length - 1][sum / 2];

    }
}

这里需要注意，我们要把第一列设置为true，因为无论你有几个数，你都能组成一个0。
这样的代码虽然直观，但是时间复杂度和空间复杂度很一般。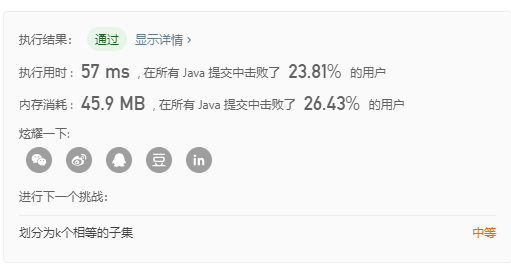
Alt text

改进1：优化数组为两行

我们可以直观的看到dp[i]依赖于dp[i-1]，那么其实我们使用一个两行的数组，即可解决这个问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public boolean canPartition(int[] nums) {
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        if (nums.length == 0) return false;
        if (sum % 2 == 1) return false;
        boolean[][] dp = new boolean[2][sum /  2 + 1];
        dp[0][0] = true;
        dp[1][0] = true;


        for (int i = 1; i < nums.length; i++) {
            for (int j = 0; j <= sum / 2; j++) {
                int num = nums[i];
                if (num > j) continue;
                dp[i % 2][j] = dp[(i - 1) % 2][j] || dp[(i - 1) % 2][j - num];
            }
        }

        return dp[(nums.length - 1) % 2][sum / 2];

    }
}

可以看到，进行优化后确实内存消耗减少了很多！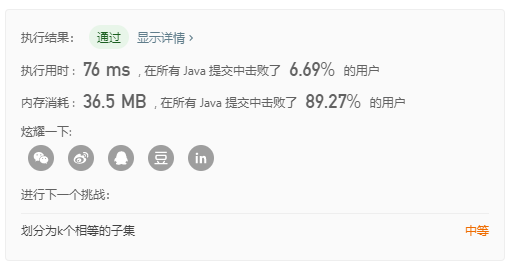
Alt text

改进2：优化数组为1行

既然两次能完成的事情，一次我也能完成，只要我从后向前完成即可，所以我们可以进一步使用一个一维数组来表示，同时，这里我们还可以提前结束。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public boolean canPartition(int[] nums) {
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        if (nums.length == 0) return false;
        if (sum % 2 == 1) return false;
        boolean[] dp = new boolean[sum /  2 + 1];
        dp[0] = true;


        for (int i = 1; i < nums.length; i++) {
            for (int j = sum / 2; j > 0; j--) {
                int num = nums[i];
                if (num > j) continue;
                if (dp[sum / 2]) return true;
                dp[j] = dp[j] || dp[j - num];
            }
        }

        return dp[sum / 2];

    }
}

Alt text

所以到这里，0/1背包问题，以及0/1背包问题的优化就完成了！

总结

  • 0/1背包问题是：物品只有一个，可以选，也可以不选！
  • 每一次都拿一个物品放进背包。